
http://www.matierevolution.fr/spip.php?article706
———————–
https://fr.wikipedia.org/wiki/Th%C3%Am9orie_du_chaos
En mathématiques, la théorie du chaos étudie le comportement des systèmes dynamiques très sensibles aux conditions initiales, un phénomène généralement illustré par l’effet papillon.
Pour de tels systèmes, des différences infimes dans les conditions initiales entraînent des résultats totalement différents, rendant en général toute prédiction impossible à long terme.
Cela concerne même les systèmes purement déterministes (ceux dont le comportement futur est entièrement déterminé par les conditions initiales, sans aucune intervention du hasard) : leur nature déterministe ne les rend pas prévisibles car on ne peut pas connaître les conditions initiales avec une précision infinie. Ce comportement paradoxal est connu sous le nom de chaos déterministe, ou tout simplement de chaos. […]
La théorie du chaos est-elle née dans les années 1970 ? La réponse à cette question est : oui et non.
– Non, car le phénomène de sensibilité aux conditions initiales a été découvert dès la fin du XIXe siècle par Henri Poincaré, dans des travaux concernant le problème à N corps en mécanique céleste (notamment dans le volume 3 des Méthodes Nouvelles de la Mécanique Céleste), puis par Hadamard avec un modèle mathématique abstrait aujourd’hui baptisé « flot géodésique sur une surface à courbure négative ». Cette découverte a entraîné un grand nombre de travaux importants, principalement dans le domaine des mathématiques. Ces travaux sont évoqués dans le paragraphe Développements historiques situé plus loin.
– Oui, car ce n’est véritablement que dans les années 1970 que la théorie du chaos s’est progressivement imposée sur le devant de la scène scientifique, opérant une rupture épistémologique forte. Le terme suggestif de « chaos » n’a d’ailleurs été introduit qu’en 1975 par les deux mathématiciens Tien-Yien Li et James A. Yorke. Otto E. Rössler, connu pour avoir découvert l’un des attracteurs chaotiques le plus étudié (et appelé aujourd’hui attracteur de Rössler), utilisa le terme de « chaos » dans la plupart de ses articles dès 1976. Le caractère tardif de ce changement de paradigme s’explique aisément : la théorie du chaos doit en effet sa popularisation aux progrès fulgurants de l’informatique à partir des années 1960-70. […]
————————————————–
Le battement d’ailes d’un papillon au Brésil peut-il provoquer une tornade au Texas ?
E. Lorenz – conférence à l’American Association for the Advancement of Science : « Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas? »
La métaphore de l’effet papillon est souvent interprétée de façon fautive. Ce n’est pas le papillon qui déclenche la tornade au Texas. Lorenz suggérait seulement que le battement d’aile du papillon peut par exemple modifier l’évolution de la tornade. Il s’agissait plutôt d’illustrer la sensibilité aux conditions « initiales » des dynamiques complexes.

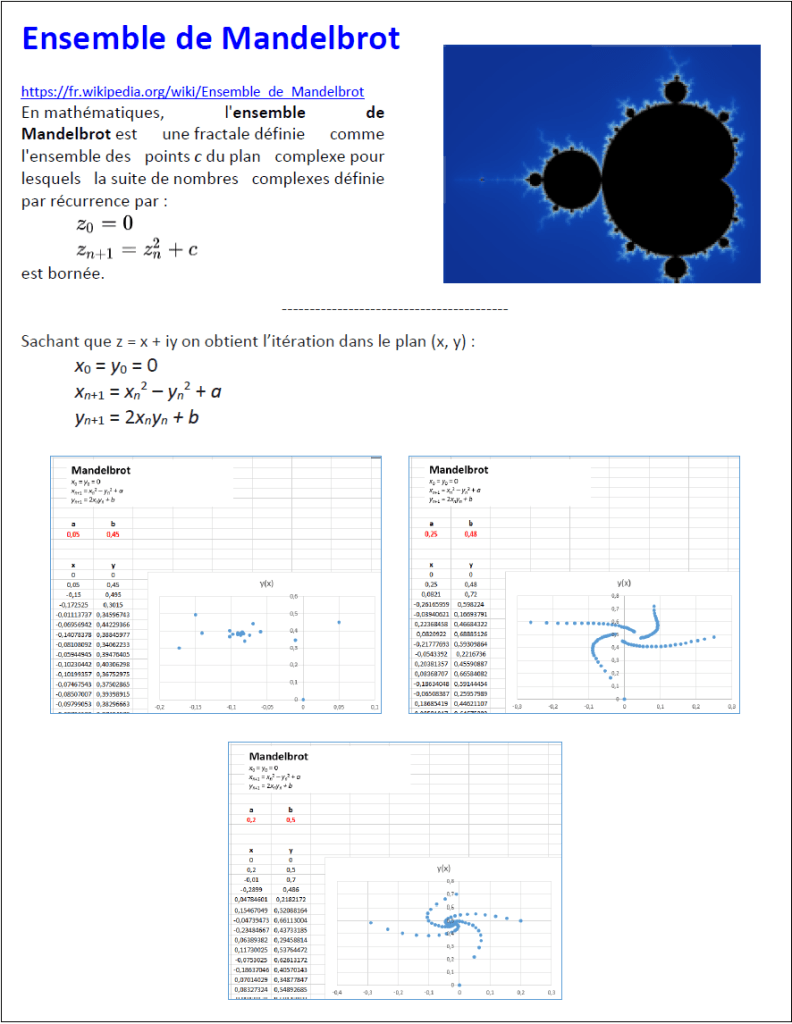
https://fr.wikipedia.org/wiki/Ensemble_de_Mandelbrot
—————————————
Une collection de documents sur les thèmes de CHAOS, BIFURCATIONS, FRACTALES…
——————————
Tous les documents indiqués sont téléchargeables à l’adresse DOCS (dossier Notes / chaos)
——————————
Un diaporama synthétique :
[1-chaos.pptx]




Et les documents :
[attracteur-henon.pdf]
[attracteur-henon.xlsx]
[bifurcations.pdf]
[bifurcations-feigenbaum.pdf]
[bifurcations-feigenbaum.xlsx]
[catastrophe.pdf]
[catastrophe.xlsx]
[convection.pdf]
[explosion.pdf]
[explosion.xlsx]
[mathematiques-chaos.pdf]
[papillon.pdf]
[fractales.pdf]
[mandelbrot.pdf]
[mandelbrot.xlsx]
[attracteurs-fractales.pdf]
[fractales-chaos.pdf]










——————————
Tous les documents indiqués sont téléchargeables à l’adresse DOCS (dossier Notes / chaos)



———————————————————————————————-