
« Galileo osserva la lampada nel Duomo di Pisa »,
affresco di Luigi Sabatelli, Tribuna di Galileo, Firenze.
Museo Galileo – Istituto e Museo di Storia della Scienza
Piazza dei Giudici 1 · 50122 Firenze · ITALIA
https://brunelleschi.imss.fi.it/itinerari/galleria/TribunaGalileo_4742.html
Son disciple et futur biographe, Vicenzio Viviani, prétend avoir recueilli de la bouche de Galilée lui-même, peu avant sa mort, le récit de son observation, quand il était encore adolescent, durant un office religieux, de la régularité des oscillations du lustre de la cathédrale de Pise (la durée d’une oscillation reste constante quelle que soit l’amplitude, c’est-à-dire la longueur de l’arc parcouru, et la vitesse croit avec celle-ci), qui l’amena à réfléchir sur la chute des corps et sur la pesanteur, et à refaire, une fois rentré chez lui, des expériences précises. Il paraît cependant, selon des esprits chagrins qui n’aiment pas les légendes, que le grand lustre ne fut installé dans la cathédrale qu’après que Galilée ait quitté Pise. […]
Reste, à propos du lustre, le fait que Galilée a bien effectué des observations sur l’oscillation des pendules pesants (en 1602), comme d’ailleurs (vers 1604) sur le temps mis à tomber par un corps placé sur un plan légèrement incliné (qui permet des mesures plus précises que la chute verticale, en ralentissant le mouvement), mesurant, en l’absence d’horloges de précision, le temps en prenant son pouls, idée empruntée au mathématicien Girolamo Cardano (Jérôme Cardan), auteur d’un grand traité d’algèbre, l’Ars Magna.
L’expérimentation, venue de la pensée technique, tient donc un rôle très important dans la pensée physique de Galilée, tributaire, par-là, de ses prédécesseurs, mais il s’agit alors des ingénieurs et des techniciens plutôt que des scientifiques. Ingénieur et mathématicien au service du Grand-Duc de Toscane, responsable de l’Arsenal, Galilée s’intéressait à des problèmes posés par des exigences techniques comme celles, très marquées aux XVIe et XVIIe siècles, de la balistique, c’est-à-dire la technique des projectiles, suscitée par l’invention des armes à feu et les besoins de l’artillerie (étude de la portée en fonction de l’angle de tir, forme de la trajectoire, etc.). Ajoutons que Galilée avait peut-être aussi été rendu sensible aux aspects pratiques par l’exemple de son père, musicien, qui faisait des expériences sur la tension des cordes de ses instruments. Michel Paty. Galilée et la mathématisation du mouvement. Passages, Brill Academic Publishers. 1996.
Salviati. J’ai pris deux boules, l’une en plomb et l’autre en liège, la première étant au moins cent fois plus lourde que la seconde, puis j’ai attaché chacune d’elles à deux fils très fins, longs tous deux de quatre coudées fixés par le haut. Puis, les écartant de la position verticale, je les ai lâchées en même temps […]. En observant une bonne centaine d’allées et venues, j’ai clairement constaté qu’entre la période du corps pesant, et celle du corps léger, la coïncidence est telle que […] le premier n’acquiert aucune avance sur le second […], mais que tous deux ont un rythme de mouvement rigoureusement identique. On observe également l’action du milieu qui, en gênant le mouvement, ralentit bien davantage les vibrations du liège que celles du plomb, sans toutefois modifier leur fréquence : même si les arcs décrits par le liège n’ont plus que cinq ou six degrés, contre cinquante ou soixante pour le plomb, les oscillations sont toujours effectuées en des durées égales. […] Notez ici deux détails qui méritent d’être connus. L’un, c’est que les vibrations de ce pendule se font en des temps si déterminés qu’il est absolument impossible de les faire s’accomplir en des temps différents, sauf en allongeant ou en raccourcissant la corde. Vous pouvez d’ailleurs vous en assurer tout de suite par une expérience : accrochez une pierre à une ficelle dont vous tenez l’autre bout en main, et essayez, par tous les moyens que vous voudrez, sauf l’allongement ou le raccourcissement de la ficelle, d’arriver à la faire osciller autrement que dans son temps déterminé ; vous verrez que c’est absolument impossible. L’autre détail est vraiment étonnant : le même pendule fait ses vibrations avec la même fréquence (du moins les différences sont très petites et presque imperceptibles), que les arcs sur cette circonférence soient très grands ou très petits. Je le déclare, que nous écartions le pendule de la verticale d’un, deux ou trois degrés seulement, ou bien de 70, 80, voire d’un angle droit, une fois qu’on l’aura laissé en liberté, dans les deux cas ses vibrations auront la même fréquence. […] Quant aux longueurs des fils constituant ces pendules, elles sont proportionnelles au carrées des temps ; si bien que pour obtenir un pendule dont le temps d’oscillation soit le double de celui d’un autre pendule, il convient de donner au premier une longueur quadruple de celle du second. De la même manière si un pendule a une longueur neuf fois supérieure à celle d’un autre pendule, le premier effectuera trois oscillations pendant que le second en accomplira une seule. […] Galilée. Discours concernant deux sciences nouvelles. 1638.
http://eaae.ens-lyon.fr/groupspace/richer-cayenne/documents-Richer/galilee.pdf
Galilée n’avait pas vu que la période dépend de l’amplitude pour de grandes oscillations. Marin Mersenne (1588-1648) relève l’erreur dans sa traduction, adaptation, compilation (Nouvelles pensées de Galilée, Liv. I, Art. XVII, Paris 1639) : « Si l’auteur eût été plus exact en ses essais, il eût remarqué que la corde est sensiblement plus longtemps à descendre depuis le haut de son quart de cercle jusqu’à la perpendiculaire (verticale), que lorsqu’on la tire seulement dix ou quinze degrés, comme témoignent les deux bruits que font deux cordes égales, frappant contre un ais (planche) mis au point de la perpendiculaire. Et s’il eût seulement nombré jusqu’à trente ou quarante retours de l’une tirée vingt degrés ou moins, et de l’autre quatre-vingts ou nonante degrés, il est connu que la moins tirée fait un retour davantage sur trente ou quarante retours ; et si l’on pouvait toujours en faire aller une à quatre-vingts degrés, tandis que celle de dix ou vingt degrés irait se diminuant, celle-ci pourrait gagner un retour sur dix ou douze retours.»
————————————————–
Tous les documents nécessaires sont téléchargeables à l’adresse DOCS (dossier mouvement (8) pendule).
———————————————
Quatre types de travaux sont proposés.
Document général : [0 pendule.pdf]
Pour chacun le document de travail principal donne les consignes pour le travail individuel et éventuellement en petits groupes. Classiquement les hypothèses ou propositions sont mises en commun en petits groupes puis en grand groupe avec animation tableau. Des corrigés sont également disponibles.
1. Galilée
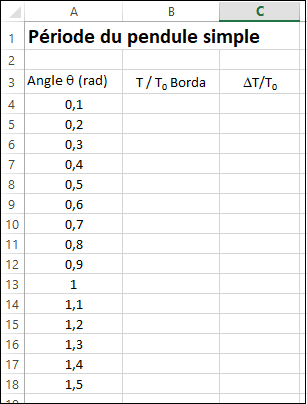
A partir des propositions de Galilée et d’autres indications on établit l’expression possible de la période du pendule (avec l’aide de l’analyse dimensionnelle. La réflexion est portée sur « l’erreur » de Galilée concernant l’isochronisme des oscillations et les incertitudes de mesure.
Documents de travail : [1-periode.pdf] ; [2-precision-galilee.pdf] ;[precision.xlsx] ainsi que le corrigé [precision-corrige.xlsx].


————————————-
2. Protocole
C’est une étude expérimentale de la période et des énergies du pendule, utilisant les résultats d’exploitation d’une vidéo.
Documents de travail : [protocole.pdf]

—————————————-
3. Pendule
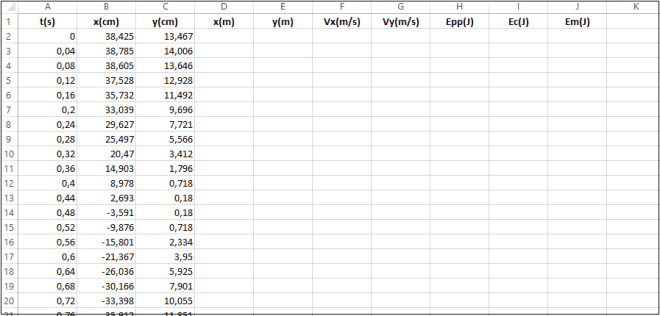
C’est une étude expérimentale de la période et des énergies du pendule, utilisant les résultats d’exploitation d’une vidéo.
Documents de travail : [1-pendule.pdf] ; [1-pendule.xslx] et le corrigé [1-pendule-corrigé.xslx]


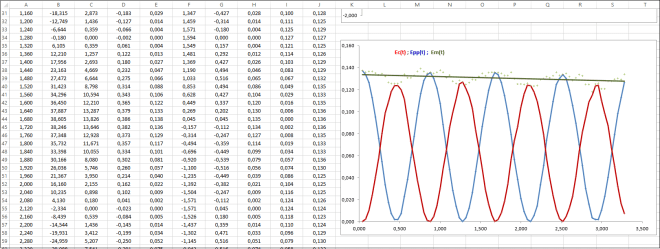
On trouvera également, dans les compléments, l’étude théorique exploitable éventuellement selon le niveau d’intervention.

——————————————-
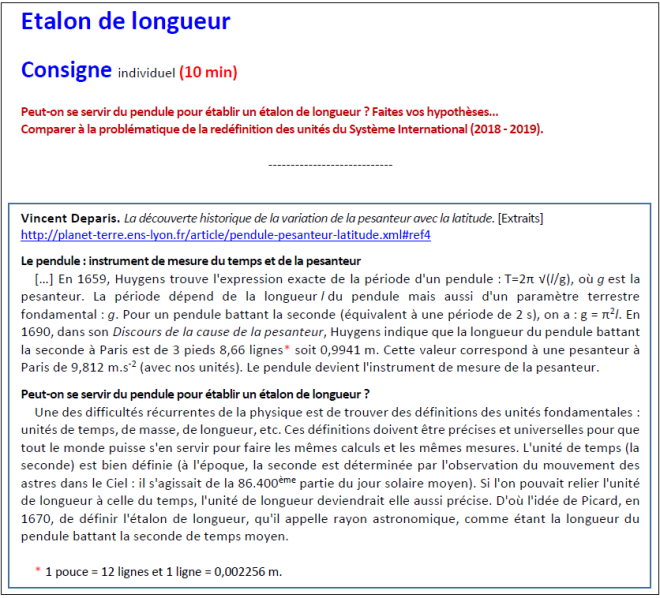
4. Étalon
Peut-on se servir du pendule pour établir un étalon de longueur ? Picard, en 1670, propose de définir l’étalon de longueur, qu’il appelle rayon astronomique, comme étant la longueur du pendule battant la seconde de temps moyen.
On compare à la problématique de la redéfinition des unités du Système International (2018 – 2019).
Documents de travail : [etalon.pdf] ; [pesanteur.pdf] ; [revision-unites.pdf].


On trouvera également un complément sur la gravimétrie : [gravimetrie.pdf] ; [geophysique-corrige.pdf].


————————————————–
Tous les documents nécessaires sont téléchargeables à l’adresse DOCS (dossier mouvement (8) pendule).






——————————————————————————-
2 commentaires sur “Mouvement (8) – Pendule”