Physique statistique, entropie et irréversibilité.
La flèche du temps fait partie de notre expérience sensible et nous en faisons l’expérience chaque jour : les miroirs brisés ne se recollent pas, les êtres humains ne rajeunissent pas, et les cernes croissent sans cesse dans les troncs des arbres… En somme, le temps s’écoule toujours dans le même sens ! Pourtant, les lois fondamentales de la physique classique ne privilégient aucune direction du temps et obéissent à une rigoureuse symétrie entre passé et futur. […] Depuis Boltzmann, la physique statistique avance une […] explication : la flèche du temps traduit un flot constant des événements moins probables vers les événements plus probables.
Cédric Villani.(Ir)réversibilité et entropie. Séminaire Poincaré XV. Le Temps (2010).
L’entropie est l’élément essentiel introduit par la thermodynamique, la science des processus irréversibles, c’est-à-dire orientés dans le temps. Chacun sait ce qu’est un processus irréversible. On peut penser à la décomposition radioactive, ou à la friction, ou à la viscosité qui ralentit le mouvement d’un fluide. Tous ces processus ont une direction privilégiée dans le temps, en contraste avec les processus réversibles tels que le mouvement d’un pendule sans friction. […] Les processus macroscopiques, tels que réactions chimiques et phénomènes de transport, sont irréversibles. Le rayonnement solaire est le résultat de processus nucléaires irréversibles. Aucune description de l’écosphère ne serait possible sans les processus irréversibles innombrables qui s’y déroulent. Les processus réversibles, en revanche, correspondent toujours à des idéalisations : nous devons négliger la friction pour attribuer au pendule un comportement réversible, et cela ne vaut que comme une approximation.
Ilya Prigogine. La fin des certitudes.
Tous les documents nécessaires sont téléchargeables à l’adresse DOCS (dossier atomisme (4)).
Document général : [0 atomisme-4.pdf]
Consigne 1 individuellement (5 min)
Supposons une équipe de foot (11 joueurs) en action et un bataillon de 11 militaires en ordre de marche.Quel est le système le plus ordonné ?

Animation tableau pour recueillir et discuter les propositions.
Consigne 2 individuellement puis en groupe (30 min)
En physique statistique la mesure du désordre d’un système correspond au nombre de façon de réaliser l’état du système à partir de ses constituants. Plus ce nombre est grand plus le système est désordonné. Ce nombre est appelé nombre de complexions et noté Ω.
En thermodynamique on définit une grandeur physique, l’entropie notée S, dont Boltzmann a donné l’interprétation statistique, en relation avec ce nombre de complexions : voir le document [entropie.pdf] entropie

Reprenons les exemples précédents.
Document disponible :[combinatoire.pdf] combinatoire

Quel est le nombre de façons de réaliser le bataillon de militaires en supposant que les militaires sont interchangeables (sauf le capitaine) ?
–Quel est le nombre de façons de réaliser l’équipe de foot en supposant que les joueurs ont chacun un rôle précis et donc ne sont pas interchangeables ?
Animation tableau et discussion.
Foot : une seule façon de réaliser l’équipe si on considère que les joueurs ne sont pas interchangeables Ω = 1. Militaires : 10 militaires interchangeables donc (10!) façons de réaliser le bataillon (c’est un calcul de permutation) ; Ω = 10! = 3 628 800. Le bataillon est donc beaucoup plus désordonné que l’équipe de foot qui, elle, est très organisée.
Consigne 3individuellement puis en groupe (50 min)
Une situation classique : la « détente de Joule – Gay-Lussac »
Supposons deux compartiments : l’un (à gauche) contient un gaz, l’autre est vide. Si on les met en communication le gaz va se répandre irréversiblement dans les deux, par le jeu des mouvements moléculaires. La probabilité pour que la totalité du gaz se retrouve dans l’un des compartiments seulement est nulle (ou presque…) !
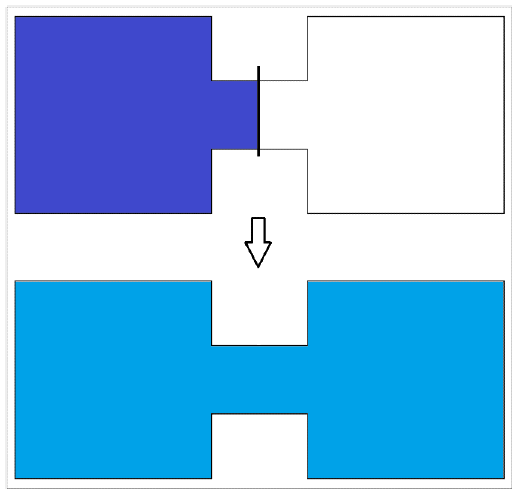
Utiliser le document de travail[detente.pdf]; detente
traiter le problème avec le tableur[probabilité.xlsx].

Rédiger une affiche avec vos premières conclusions.
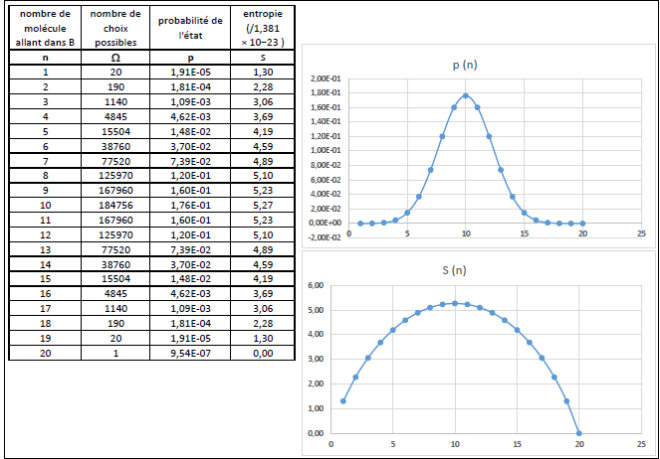
Lorsque vous aurez accès aux résultats [probabilite corrige.xlsx] comparer les résultats pour 20 et 1000 molécules et compléter l’affiche avec vos conclusions. Que se passe-t-il pour un nombre de molécules de l’ordre de la Constante d’Avogadro (6,02 x 1023) ?

Affichage et présentations de plusieurs affiches. Animation tableau pour
la mise au point.
On constate évidemment que la probabilité maximum correspond à un nombre égal de molécules dans les deux compartiments. Plus le nombre de molécules est grand, plus les fluctuations sont faibles, et sont totalement négligeables pour un nombre de molécules de l’ordre de grandeur de la !constante d’Avogadro.
Magistral. Physique statistique et entropie statistique. Irréversibilité et flèche du temps.
Tous les documents nécessaires sont téléchargeables à l’adresse DOCS (dossier atomisme (4)).
