Mouvement (9) – Kepler

https://fr.wikipedia.org/wiki/Johannes_Kepler#Le_Mysterium_Cosmographicum

Poursuivi pour ses convictions religieuses et ses idées coperniciennes, Johannes Kepler doit quitter Graz en 1600. Il se réfugie à Prague, invité par l’astronome danois Tycho Brahe pour y devenir son assistant. Les relations entre les deux personnages furent particulièrement houleuses, Tycho Brahe ne croyant pas à l’héliocentrisme de Nicolas Copernic mais soutenant une autre théorie dans laquelle la Terre est au centre mais les autres planètes tournent autour du Soleil. […]

Brahe lui demanda de calculer l’orbite précise de Mars, dont les positions suivant ses observations résistaient à toute tentative de modélisation, et s’écartaient notablement (de plusieurs degrés) de celles prévues par les tables. […] Il pensait accomplir sa tâche en quelques semaines, mais il lui fallut près de six ans pour achever son travail. C’est durant ce travail que Johannes Kepler découvrit les deux premières des trois lois fondamentales :

· Les planètes décrivent des trajectoires elliptiques dont le Soleil est un foyer.

· Le mouvement de chaque planète est tel que le segment de droite reliant le Soleil et la planète balaie des aires égales pendant des durées égales.

Ces lois furent publiées dans Astronomia Nova en 1609, où Johannes Kepler fut également le premier à émettre l’hypothèse d’une rotation du Soleil sur son axe. En 1618 viendra sa troisième grande loi :

· Pour toutes les planètes, le rapport entre le cube du demi grand axe de la trajectoire et le carré de la période est le même – cette constante est indépendante de la masse de la planète.

En fait, la révolution astronomique s’accomplit en trois étapes, liées, chacune, à l’œuvre d’un homme : avec Copernic, qui arrête le Soleil et lance la Terre dans les cieux, l’héliocentrisme se substitue au géocentrisme. Avec Kepler, la dynamique céleste – hélas, aristotélicienne – remplace la cinématique des cercles et des sphères de Copernic et des Anciens. De ce lait, même la hantise de la circularité se trouve partiellement – dans un monde clos elle ne peut l’être entièrement –  surmontée et l’astronomie elliptique fait son entrée triomphale dans le monde. Enfin, avec Borelli, dans un monde désormais ouvert et régi par la dynamique, s’achève l’unification de la physique céleste et de la physique terrestre qui se traduit par la déroute du cercle au profit de la droite infinie. 

A. Koyre. La révolution astronomique. 1961.

Johannes Kepler (1571 – 1630)

Les solides platoniciens et les sphères des planètes. Une inspiration illumine la pensée de Kepler : il faut passer de deux à trois dimensions, du cercle à la sphère, des polygones aux polyèdres. Il n’existe que cinq polyèdres réguliers (connus depuis des siècles sous le nom de «solides platoniciens») et six planètes dans le Système solaire copernicien. Ainsi, Kepler imagine un Système solaire «à emboîtement», où les sphères qui représentent les orbites des planètes alternent avec des solides idéaux parfaits dont, pour chacun, la sphère tangente intérieure symbolise la sphère «orbitale» d’une planète et la sphère extérieure, celle de la planète suivante (dans l’ordre des distances par rapport au Soleil). […] 

Kepler aborde alors la dernière étape de son parcours vers une Harmonie céleste, qui le conduira à sa «troisième loi». Il est désormais inévitable de rechercher une dépendance harmonique entre les rayons moyens des orbites des planètes et les vitesses de celles-ci. D’une part, la tradition soutient qu’il existe une relation entre les rayons des orbites et les intervalles musicaux, mais Kepler démontre qu’il est impossible de les relier directement ; d’autre part, il met en évidence l’Harmonie qui relie les vitesses minimales et maximales des planètes. Ainsi, le lien entre les rayons des orbites et l’Harmonie doit passer par les vitesses, plus précisément par une loi proportionnelle entre les vitesses (et donc, les périodes de révolution) et les rayons des orbites. 

Anna Maria Lombardi. Les génies de la science N°8 – Août 2001. Revue pour la science.

Johannes Kepler

MysteriumCosmographicum, Tübingen 1596.

————————————————

Tous les documents  nécessaires sont téléchargeables à l’adresse DOCS (dossier mouvement (9) kepler).

———————————————————

L’étude proposée exploite la troisième loi de Kepler.

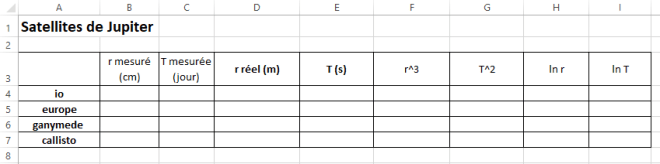
Il s’agit de déterminer la masse du Soleil (on donne les périodes et rayons d’orbite des planètes) puis celle de Jupiter (on utilise un graphique de l’éphéméride mensuelle des satellites médicéens de Jupiter).

Documents de travail (dossier [masse]) :

[0-attracteur.pdf] ; [1-soleil.xlsx]; [2-jupiter.pdf] ; [2-jupiter.xlsx]

Des corrigés sont également disponibles.

1-soleil-corrige ; 2-jupiter-corrige

Divers documents complémentaires sont aussi proposés (textes, diaporamas, animation…) :

[2-jupiter.pptx], [kepler-laws.swf] et ceux des dossiers [textes] et [complements].

systemes-du-monde ; newton ; distances ;

harmonie ; kepler ; aristarque1…