Energie (2) – Unificateur

L’énergie : un
concept unificateur.

PETIT TRAITÉ DE PHYSIQUE à l’usage des Etablissements d’Instruction, des aspirants aux
Baccalauréats et des candidats aux Ecoles du Gouvernement. M. J. JAMIN – Paris – 1870

————————————————————————————————————-

Mais c’est à Newton qu’il devait revenir d’exprimer les lois dynamiques pour un instant donné en relation à un instant quelconque, grâce à la pensée du calcul infinitésimal qui est implicite dans la géométrie des limites mise en œuvre dans les Principia. La formulation des lois du mouvement et de la dynamique connut ainsi son aboutissement avec Isaac Newton, qui en fit un système, couronné par sa découverte de la loi de la gravitation universelle. Reprenant les trois lois déjà formulées avant lui de l’inertie, de la composition des mouvements et des forces, et de l’équilibre ou de l’action et de la réaction, il les formula de manière systématique et en termes de forces, unifiant ce concept autour de sa seconde loi, qui exprime le changement de vitesse en fonction de la force appliquée¹. C’est la loi fondamentale de la dynamique newtonienne, ultérieurement traduite dans la symbolique du calcul différentiel et intégral leibnizien, qui constitue la loi, différentielle et causale, de la dynamique de corps matériels. 

Michel Paty. Histoire rapide de la vitesse (le concept physique).

¹

———————————

C’est cependant l’emploi croissant du langage mathématique qui a conditionné les progrès majeurs d’où le concept d’énergie mécanique s’est dégagé. Un moment crucial est la publication en 1788 de la Mécanique analytique de Louis de Lagrange (Turin 1736 – Paris 1813). Peu intéressé par des discussions philosophiques, celui-ci élabore un formalisme unifié basé sur l’emploi du calcul différentiel. Il déduit des équations du mouvement le « théorème des forces vives » : au cours d’un processus non dissipatif, le travail reçu par chaque point matériel (de masse m et de vitesse v) d’un système est égal à la moitié de l’accroissement de sa force vive mv². Afin de passer de là à la conservation de l’énergie mécanique, somme des énergies potentielle V et cinétique T, il restait à reconnaître que les forces appliquées au système dérivent en général d’un potentiel, à en déduire que leur travail s’identifie à la diminution d’une certaine fonction V des variables de position appelée plus tard « énergie potentielle » (William Rankine, 1853), et
à interpréter la demi force vive T=½∑mv² comme « énergie cinétique » (Gaspard-Gustave Coriolis, 1829). Plusieurs décennies seront nécessaires pour établir clairement que l’énergie mécanique totale T+V reste constante au cours du temps en l’absence de dissipation.

Roger Balian. La longue élaboration du concept d’énergie. http://www.academie-sciences.fr/archivage_site/activite/hds/textes/evol_Balian1.pdf

———————————-

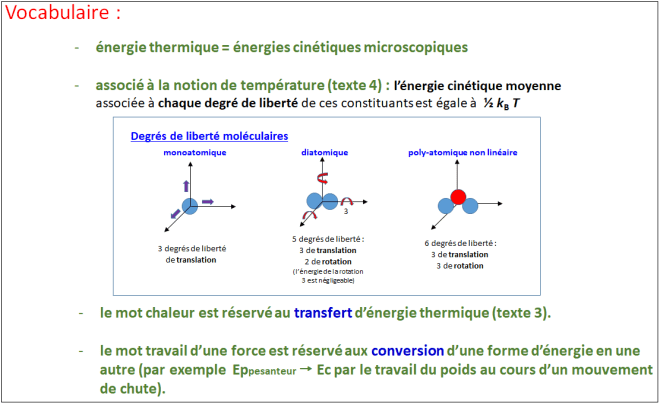
[…] on sait depuis les travaux de Maxwell et Boltzmann au XIXe siècle, que la température est susceptible d’une définition microscopique : elle est une mesure de l’agitation thermique des constituants « atomiques » de la matière, indépendante de la nature chimique de ces constituants. Plus précisément, pour un corps maintenu à la température T, l’énergie cinétique moyenne associée à chaque degré de liberté de ces
constituants est égale à ½ k_BT(théorème dit d’équipartition de l’énergie), où k_B est une des constantes fondamentales de la physique, appelée constante de Boltzmann. Le point essentiel est qu’au niveau microscopique la grandeur susceptible d’une interprétation physique est, non pas la température T elle-même, mais le produit k_BT. http://archive.wikiwix.com/cache/url=http%3A%2F%2Fwww.cnrs.fr%2Fpublications%2Fimagesdelaphysique%2Fcouv-PDF%2FIdP2006%2F13_Constante_de_Boltmann.pdf

 

——————————————————–

Partie 1 : le théorème des « forces vives » (ou théorème de l’énergie cinétique).

Pourquoi a-t-on été amené à définir l’énergie cinétique (d’un point matériel de masse m) par : 

E_c = ½ m V²      ?

Il s’agit ici de retrouver le théorème de l’énergie cinétique à partir de la seconde loi de Newton par la démonstration théorique. Les consignes sont portés sur le document de travail : [energie cinetique.pdf].

 

La consigne 1 est suivie d’une mise en commun avec animation tableau pour les mises au point. Elle conduit à F = dp /dt donc F = m a (dite seconde loi de Newton ou relation fondamentale de la dynamique) pour un objet de masse m constante (p : quantité de mouvement, a : accélération = dV / dt) les grandeurs utilisées étant plus généralement vectorielles.

On pourra également exploiter antérieurement l’atelier Ignorato motu, disponible sur ce même site, pour la construction des lois fondamentales de la mécanique de Newton (en particulier la seconde loi).

La consigne 2 est suivie d’une mise en commun en petit groupe (10 min) puis d’une animation tableau pour le recueil des propositions et les mises au point.

Conclusion et généralisation vectorielle à partir du document [tec.pptx] (et [tec.pdf]) et retour sur le texte de Mach.

——————————————————–

Partie 2 : forces conservatives et énergies potentielles.

La construction historique du concept d’énergie passe par l’élaboration de la notion l’énergie potentielle (vis potentialis) comme le montre le texte [vis potentialis.pdf].

L’activité proposée ici propose de retrouver les expressions des énergies potentielles de pesanteur et élastiques à partir des calculs des travaux des forces correspondantes. Le fait que ces travaux soient indépendants du « chemin suivi » permet de définir les énergies potentielles. On élabore alors une première expression de conservation de l’énergie « mécanique ».

Les consignes sont portées sur le document de travail : [energies potentielles.pdf].

On pourra illustrer le propos en fin ou en cours de travail avec l’animation: [oscillateur elastique.swf]. On pourra également conclure avec le diaporama : [travail et energie (1).pptx].

 

La consigne 2 est suivie d’une mise en commun avec animation tableauà partir de la présentation d’affiches pour les mises au point.

On obtient : W(P)_AB = P . AB cos (P, AB) = P (Z_A – Z_B) = m g Z_A – m g Z_B

On voit que le résultat est indépendant du chemin suivi.

Le théorème de l’énergie cinétique appliqué au mouvement de chute verticale
sans frottement donne : DEc = ½ m V_B² – ½ m V_A² = W(P)_AB = m g Z_A – m g Z_B

Alors                    ½ m V_B² – ½ m V_A² = m g Z_A – m g Z_B

donc                    ½ m V_B² + m g Z_B = ½ m V_A² + m g Z_A

La somme des deux termes est donc conservée au cours de la chute ans frottement. Alors on appelle énergie potentielle de pesanteur la quantité Epp = m g Z

D’où la loi de conservation (en l’absence de frottement) : Ec + Epp = constante = Emécanique.

Pour la consigne 3 on relève les propositions individuelles sous forme d’animation tableau pour la mise au point.

Consigne 4. Reprise des propositions en animation tableau. L’analyse dimensionnelle donne :

Dim(Ec) = M L² T^-2

Dim(Epp) = Dim(m g Z) = M L T^-2 L = M L² T^-2

Dim (Epe) = Dim (k x²) = (Dim (F) / L ) L² = (M L T^-2 /L ) L² = M L² T^-2

Donc dans les trois cas dimension de l’énergie et unité le Joule.

De même pour la consigne 5 on reprend les propositions en animation tableau ;

Descartes et Leibniz s’oppose sur la définition de ce qui caractérise « l’intensité », la « force » d’un mouvement : quantité de mouvement mv pour Descartes ; force vive (vis viva) mV² pour Liebniz.

Le terme « force » ne correspond pas à la notion actuelle de force (action d’un objet sur un autre) mais plutôt à l’idée actuelle d’énergie ; Vis viva : énergie cinétique
(1/2 vis viva) ; vis potentialis : énergie potentielle.

Lorsqu’on lance un objet verticalement vers le haut la vis viva (Ec) diminue jusqu’à s’annuler et la vis potentialis (Epp) augmente (et inversement à la descente) ; mais l’ensemble des deux est constant (en l’absence de frottement). La description est analogue pour le système élastique-masse ; ressort étiré ou comprimé : vis potentialis (Epe) ; masse en mouvement : vis viva (Ec).

 

——————————————————–

Partie 3 : le « drame » dissipatif.

Diverses situations concrètes montrent que l’énergie mécanique n’est pas constante : chute dans l’air, amortissement des oscillations du pendule pesant ou du pendule élastique, arrêt des mouvements non entretenus par un moteur… Le mouvement perpétuel est impossible !!!

On se propose d’analyse la situation du pendule amorti pour montrer la non conservation de l’énergie mécanique et s’interroger sur sa transformation.

Le document de travail [dissipatifs.pdf] donne les consignes.

On utilisera les animations :[pendule1.swf] et [pendule2.swf]

En conclusion magistrale on pourra utiliser les diaporamas : [energie pendule.pptx] et
[travail et energie (2).pptx]

 

Consigne 1 : graphes des oscillations (abscisse angulaire à préciser sans doute) et graphes d’énergies (Ec, Epp, Em) ; avec frottement on observe l’amortissement des
oscillations et la diminution des énergies ; les frottements entraînent la « dissipation » de l’énergie mécanique (chaleur ? ou plutôt énergie thermique).

Consigne 2 : W(f)_AB = f . AB = f AB cos p = – f AB < 0 travail résistant

Consigne 3 : présentation de plusieurs affiches et animation tableau pour les mises au point.

——————————————————–

Partie 4 : macro et micro, l’unification des concepts.

On a vu précédemment que deux types d’énergie peuvent être définis à notre échelle macroscopique : l’énergie cinétique d’un objet (ou d’un ensemble d’objets) en mouvement (Ec = S ½ m V²) et les énergies potentielles correspondant aux forces conservatives subies par les objets (gravitation, force électrique, force élastiques…)

Et ces concepts d’énergie permettent de formuler une loi de conservation : pour un système isolé (sans action de forces extérieures) et conservatif (pas de frottements…) la somme de ces énergies (énergie mécanique) est constante.

Mais que devient l’énergie s’il y a des frottements ? D’où vient l’énergie cinétique produite par un moteur à combustion ? D’où provient l’énergie potentielle électrique d’une pile ?

L’objectif est de généraliser la loi de conservation en faisant appel aux modèles microscopiques.

Le document de travail [macro-micro.pdf] porte les consignes et les textes utilisés.

 

Le diaporama [energie macro micro.pptx] permet une synthèse magistrale en fin de travail.

Compléments disponibles : [energie.swf] (très bonne animation de André Willm) ; [transferts thermiques.pptx].

On pourra également exploiter, disponible sur ce même site, les chantiers de sciences :

Atomisme (2) Température, chaleur et controverses historiques.

Atomisme (3) Théorie cinétique des gaz ou comment décrire le chaos.

Atomisme (4) Physique statistique, entropie et irréversibilité.

La mise au point se fait à partir de la présentation des affiches, par animation tableau.

Les consignes 1, 2 et 3 permettent d’élaborer les éléments suivants : 

• La chaleur n’est pas une substance mais correspond à l’agitation moléculaire, atomique… 
• Précision de vocabulaire : énergie thermique = énergie cinétique microscopique ; le mot chaleur est réservé au transfert d’énergie thermique ; ainsi se généralise notion d’énergie cinétique du niveau macroscopique au niveau microscopique. 
• Pour les réactions chimiques on introduit la notion d’énergie potentielle au niveau microscopique (interactions atomiques, ioniques…

Voir pour la synthèse le diaporama [energie macro micro.pptx].

——————————————————–