Mouvement (2) – Plans inclinés

Galilée démontrant la loi de la chute des
corps à Don Giovanni de Medici

Museo Galileo – Istituto e Museo di Storia della Scienza
Piazza dei Giudici 1 · 50122 Firenze · ITALIA 

http://scenari.crdp-limousin.fr/galilee/co/module_galilee_8.html

Dans une règle, ou plus exactement un chevron de bois, long d’environ 12 coudées, large d’une demi-coudée et épais de 3 doigts, nous creusions un petit canal d’une largeur à peine supérieure à un doigt, et parfaitement rectiligne ; après l’avoir garni d’une feuille de parchemin bien lustrée pour le rendre aussi glissant que possible, nous y laissions rouler une boule de bronze très dure, parfaitement arrondie et polie. Plaçant alors l’appareil dans une position inclinée, en élevant l’une de ses extrémités d’une coudée ou deux au-dessus de l’horizon, nous laissions, comme je l’ai dit, descendre la boule dans le canal, en notant, selon une manière que j’exposerai plus loin, le temps nécessaire à une descente complète : l’expérience était recommencée plusieurs fois afin de déterminer exactement la durée du temps, mais sans que nous découvrîmes jamais de différence supérieure au dixième d’un battement de pouls. […]  On doit d’abord prendre garde que quelle que soit l’inclinaison du plan sur lequel le mobile, partant du repos, augmente sa vitesse […] proportionnellement au temps (selon la définition du mouvement naturellement accéléré donné par l’Auteur), les espaces parcourus sont toujours comme les carrés des temps, et donc des degrés de vitesse, ainsi que la proposition précédente l’a montré […].

Galilée. Discours concernant deux sciences nouvelles. 1638.

La loi de la chute des corps, qui a sonné le glas de la physique aristotélicienne, comporte deux assertions qui, bien qu’étroitement liées dans l’esprit de Galilée, ne sont pas moins indépendantes l’une de l’autre et doivent, de ce fait, être soigneusement distinguées. La première concerne la structure mathématique et dynamique du mouvement de la chute. Elle affirme que ce mouvement obéit à la loi du nombre et que les espaces traversés dans des intervalles successifs (et égaux) du temps sont ut numeri impares ab unitate (1) ; en d’autres termes, qu’une force constante, à l’encontre de ce qu’avait enseigné Aristote, détermine non pas un mouvement uniforme, mais un mouvement uniformément accéléré (2), c’est-à-dire que l’action de la force motrice produit non pas une vitesse, mais une accélération. La deuxième ajoute que dans leur mouvement de chute, également à l’encontre d’Aristote, tous les corps, grands et petits, lourds et légers, c’est-à-dire quelles que soient leurs dimensions et leurs natures, tombent, en principe, sinon en fait (3), avec la même vitesse ; en d’autres termes, que l’accélération de la chute est une constante universelle (4).

(1) Dans le mouvement de la chute, les vitesses croissent proportionnellement au temps, c’est-à-dire, comme les nombres ; les espaces parcourus, dans les intervalles successifs, comme les nombres impairs ; et les espaces parcourus depuis le commencement de la chute, comme les carrés.

(2) En dernière analyse, la loi de la chute des corps implique celle d’inertie, c’est-à-dire, de la conservation du mouvement. Pour Aristote, on le sait bien, une telle conservation est impossible : le mouvement implique l’action d’une force motrice, d’un moteur attaché au mobile : séparé du premier, le second s’arrête.

(3) Vu la résistance de l’air, l’égalité de la vitesse de la chute des corps graves et légers ne pourrait avoir lieu que dans le vide.

(4) Pour nous — comme déjà pour Kepler — qui réduisons la gravité à l’attraction terrestre, cette « constante » varie avec l’éloignement du grave du centre de la Terre. Pour Galilée, qui n’admet pas d’attraction, la constante d’accélération a une valeur universelle. Cette constance est, d’ailleurs, impliquée dans la déduction même de la loi de la chute par Galilée.

Alexandre Koyre. Le De Motu Gravium de Galilée. De l’expérience imaginaire et de son abus. In: Revue d’histoire des sciences et de leurs applications, tome 13, n°3, 1960. pp. 197-245

A propos de l’établissement de la loi de la chute libre, dont la vitesse augmente avec le mouvement du corps – ce qui était déjà connu -, Galilée se proposa d’en trouver l’expression mathématique et observa que les distances parcourues sont comme les carrés des temps écoulés. Il lui fut plus difficile d’en trouver l’explication: il posa d’abord que la distance est tout simplement proportionnelle à la vitesse de chute. Puis il s’aperçut – trois ans après – qu’elle variait avec le carré de la vitesse de chute, et tenait ainsi la raison de la loi. Mais il crut encore un certain temps que la vitesse de chute dépendait de la nature du corps (qu’elle était proportionnelle à sa densité), en cela tributaire, mais seulement en partie, d’Aristote, pour qui elle était proportionnelle à la grosseur du corps (c’est-à-dire à sa taille et à son poids), avant de se rendre compte qu’elle était la même pour tous les corps. Michel Paty. Galilée et la mathématisation du mouvement. Brill Academic Publishers, 1996, pp.49-53.

————————————————

Tous les documents  nécessaires sont téléchargeables à l’adresse DOCS (dossier mouvement (2) plans-inclines).

———————————————

Il s’agit ici de « reproduire » l’étude de Galilée et exploiter les résultats. On peut envisager différents dispositifs exploitables :

—————————————–

Deux études sont proposées.

1. Etude théorique et simulation

Documents de travail : [simulation-theorie.pdf] et [simulations.xslx]

Documents d’aide : [theorie.pptx]

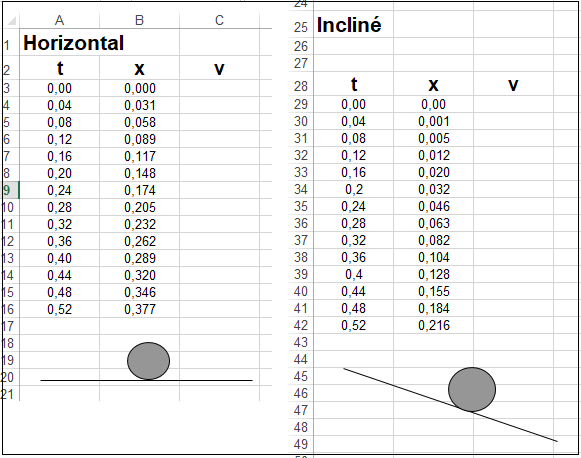
Il s’agit d’utiliser la seconde loi de Newton pour montrer que, si les frottements sont négligeables :

– sur le plan horizontal l’accélération est nulle et la vitesse constante ;

– sur le plan incliné a = g sin a.

Le document de simulation permet de mettre en œuvre les calculs de vitesse et insertions de graphes correspondant aux modélisations théoriques idéalisées.

2. Etude expérimentale

On utilise ici l’exploitation d’une vidéo du chariot sur plan incliné. Si on dispose d’un outil d’exploitation on peut évidemment traiter le clip [plan-incliné.avi].

Documents de travail : [discours.pdf]et [plan-incline.pdf]

Documents complémentaire : [g-sinalpha.xls]

Le document [discours.pdf]donne à analyser le texte de Galilée extrait de Discours sur deux sciences nouvelles. Il s’agit d’extraire les éléments clés de la démarche expérimentale de Galilée ainsi que les résultats qu’il obtient.

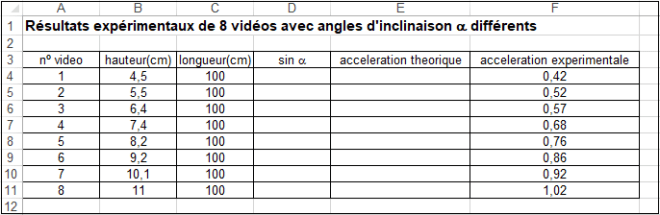
Le document [plan-incline.pdf] donne les résultats expérimentaux obtenus à partir de l’exploitation de la vidéo ainsi que la consigne de travail individuel : il s’agit de retrouver la valeur de g en utilisant deux des résultats.

Enfin, le document [g-sinalpha.xlsx] donne les résultats expérimentaux pour diverses inclinaisons du plan et permet de confronter la théorie (idéalisée sans frottement) avec l’expérience.

Compléments :

[distance-temps.pdf]. Les espaces parcourus, dans les intervalles successifs, comme les nombres impairs ; et les espaces parcourus depuis le commencement de la chute, comme les carrés.

[koyre.pdf]. Analyses d’Alexandre Koyré.

Ainsi que : [paty.pdf] et [thuillier].