Mouvement (1) – Vitesse

Vitesse-performances-speed-©-Wong-Sze-Fei-Fotolia.com

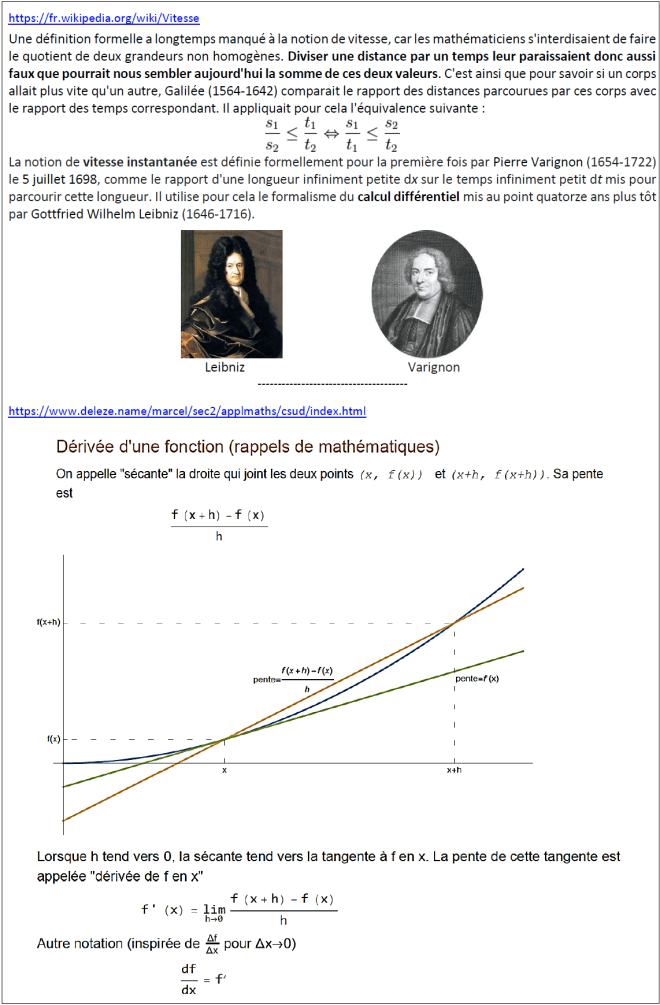
La notion de vitesse instantanée est définie formellement pour la  première fois par Pierre Varignon (1654-1722) le 5 juillet 1698, comme le rapport d’une longueur infiniment petite dx sur le temps infiniment petit dt mis pour parcourir cette longueur. Il utilise pour cela le formalisme du calcul différentiel mis au point quatorze ans plus tôt par Gottfried Wilhelm Leibniz (1646-1716).

Varignon (1654-1722) 

Leibniz (1646-1716) 

————————————-

https://fr.wikipedia.org/wiki/Paradoxes_de_Z%C3%A9non

Dans le paradoxe d’Achille et de la tortue, il est dit qu’un jour, le héros grec Achille a disputé une course à pied avec le lent reptile. Comme Achille était réputé être un coureur très rapide, il avait accordé gracieusement à la tortue une avance de cent mètres. Zénon affirme alors que le rapide Achille n’a jamais pu rattraper la tortue. « En effet, supposons
pour simplifier le raisonnement que chaque concurrent court à vitesse constante, l’un très rapidement, et l’autre très lentement ; au bout d’un certain temps, Achille aura comblé ses cents mètres de retard et atteint le point de départ de la tortue ; mais pendant ce temps, la tortue aura parcouru une certaine distance, certes beaucoup plus courte, mais non nulle, disons un mètre. Cela demandera alors à Achille un temps supplémentaire pour parcourir cette distance, pendant lequel la tortue avancera encore plus loin ; et puis une autre durée avant d’atteindre ce troisième point, alors que la tortue aura encore progressé. Ainsi, toutes les fois où Achille atteint l’endroit où la tortue se trouvait, elle se retrouve encore plus loin. Par conséquent, le rapide Achille n’a jamais pu et ne pourra jamais rattraper la tortue.

La formalisation de la notion de vitesse en une grandeur quantitative, caractérisée par une valeur numérique, est intervenue fort tardivement, à l’extrême fin du XVII^e siècle, avec Pierre Varignon. Nous sommes désormais accoutumés à définir la vitesse (moyenne) d’un mobile entre deux instants comme le rapport de la distance parcourue au temps de parcours. Mais il faut s’efforcer de saisir, malgré la familiarité acquise en quatre siècles avec cette idée, ce qu’elle contient de radicalement novateur. Une chose est de constater, banalement, qu’un coureur qui parcourt 10 km en une heure va plus vite que le marcheur qui en parcourt 5. Une autre est de décider que, par définition, la vitesse du premier vaut 10 km/h et celle du second 5 km/h, autrement dit, d’utiliser le rapport d’une longueur (le kilomètre) et d’un temps (l’heure) comme unité de mesure. C’est que, jusque-là, on n’établissait de rapports qu’entre grandeurs de même nature ; la théorie des proportions d’Euclide permet de comparer entre elles des longueurs, par exemple, et de dire que telle distance est trois fois plus grande que telle autre : leur rapport est de trois. Mais établir un rapport entre grandeurs de natures différentes et voir émerger ainsi une unité de mesure secondaire combinée, ici le « kilomètre par heure », voilà qui constitua une véritable révolution épistémologique. […] Jean-Marc Lévy-Leblond. Les avatars de la vitesse. Le Genre humain2010/1 (N° 49).

——————————————————————

L’étude expérimentale des mouvements est évidemment confrontée au calcul de la vitesse instantanée comme, selon Varignon, « le rapport d’une longueur infiniment petite dx sur le temps infiniment petit dt mis pour parcourir cette longueur ». L’infiniment petit s’avère difficilement accessible à l’expérience !

Mais en tous cas les dx et dt doivent être les plus petits possibles…

Selon le Programme de physique-chimie de seconde générale et technologique (2019), on peut « approcher le vecteur vitesse d’un point à l’aide du vecteur déplacement MM’, où M et M’ sont les positions successives à des instants voisins séparés de Δt. »

——————————————————————

Document général et commentaires : [0-vitesse.pdf] ; [commentaires.pdf]

——————————-

Deux travaux sont proposés ici.

1. Cinématique-1

document de travail : [cinematique-1.pdf]

document d’aide : [definitions.pdf]

Il s’agit de distinguer différents types de mouvements et d’approcher les calculs de vitesse et leur tracé vectoriel (« à la main ») sur des enregistrements de mobiles autoporteurs. Le document de travail porte la consigne du travail individuel. ce dernier sera suivi d’une mise en commun des propositions en petits groupes puis en grand groupe sous forme d’animation tableau.

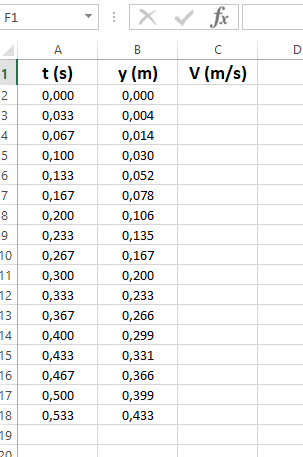
document de travail : [cinematique-2.pdf] et [resultats.xlsx]

documents complémentaires : [bille.avi] ; [rappels-tableur.pptx] 

Si on dispose d’un outil de traitement de vidéo on pourra évidemment utiliser le clip [bille.avi]. 

Le document de travail donne la consigne de travail individuel. Là aussi il sera suivi d’une mise en commun des propositions en petits groupes puis en grand groupe sous forme d’animation tableau. Il s’agit d’exploiter le fichier [resultats.xlsx] pour obtenir les valeurs de vitesse est les graphes de position et vitesse en fonction du temps.

On trouvera aussi deux corrigés correspondant à deux méthodes de calcul de la vitesse évoqués plus loins.

—————————————-

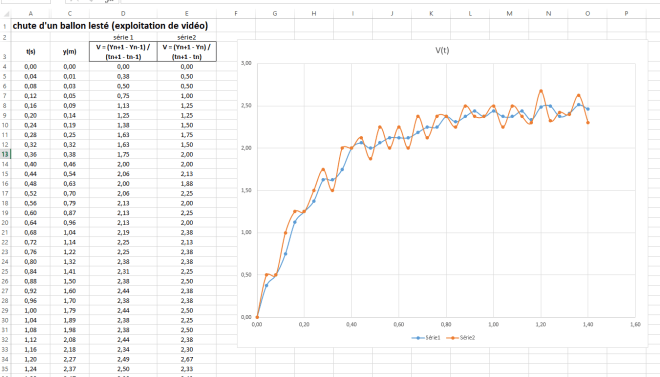
Les documents proposées dans le dossier [exemples-critiques] (avec leurs corrigés) interrogent les modes de calcul ou de tracés vectoriels de la vitesse, dans des conditions expérimentales ou de simulation théorique, où (t_i+1 – t_i) = Dt, intervalle de temps constant d’enregistrement expérimental ou de simulation :

V_i= (x_i+1 – x_i-1) / (t_i+1 – t_i-1)

ou alors :

V_i = (x_i+1 – x_i) / (t_i+1 – t_i)

ou bien :

V_i = (x_i – x_i-1) / (t_i – t_i-1)

La simulation de la chute libre sans frottement, [exemple1.xlsx], donne un résultat intéressant mais non généralisable. Evidemment la dérivée de la fonction X = ½ g t² donne v = g t. En effet, par définition de la dérivée (lim signifiant limite lorsque dt tend vers 0) : dy/dt = lim (½ g [(t+dt)² – t²] / dt = lim (½ g (t²+ 2 t dt + dt² – t²) / dt = lim (½ g (2 t dt + dt²) / dt = lim (gt + dt) = gt.

Si on fait le calcul avec la première relation on obtient :

V_i = ½ g (t_i+1²– t_i-1²) / (t_i+1 – t_i-1) = ½ g (t_i+1+ t_i-1) = ½ g 2 t_i = g t_i

Ce qui donne un résultat exact.

Si on fait le calcul avec la deuxième relation on obtient :

V_i = ½ g (t_i+1²– t_i²) / (t_i+1 – t_i) = ½ g (t_i+1+ t_i) = ½ g (2 t_i + Dt) = g t_i + ½ g Dt

L’erreur relative produite est donc ½ Dt / t_i, d’autant plus grande que t_i est petit.

Deux exemples comparables, de types expérimentaux, permettent également de déceler les écarts de résultats obtenus selon les modes de calcul : [exemple2.xlsx] et [exemple3.xlsx].

Enfin l’approche vectorielle est également questionnée avec le document [vecteur-vitesse.pdf].